Повышение эффективности зa счет добавления вычисленных фактов к базе данных
Иногда в процессе вычислений приходится одну и ту же цель достигать снова и снова. Поскольку в Прологе отсутствует специальный механизм выявления этой ситуации, соответствующая цепочка вычислений каждый раз повторяется заново.
В качестве примера рассмотрим программу вычисления N-го числа Фибоначчи для некоторого заданного N. Последовательность Фибоначчи имеет вид:
1, 1, 2, 3, 5, 8, 13, ...
Каждый член последовательности, за исключением первых двух, представляет собой сумму предыдущих двух членов. Для вычисления N-гo числа Фибоначчи F определим предикат
фиб( N, F)
Нумерацию чисел последовательности начнем с N = 1. Программа для фиб обрабатывает сначала первые два числа Фибоначчи как два особых случая, а затем определяет общее правило построения последовательности Фибоначчи:
фиб( 1, 1). % 1-е число Фибоначчи
фиб( 2, 1). % 2-е число Фибоначчи
фиб( N, F) :-
% N-е число Фиб., N > 2
N > 2,
N1 is N - 1, фиб( N1, F1),
N2 is N - 2, фиб( N2, F2),
F is F1 + F2.
% N-e число есть сумма двух
% предыдущих
Процедура фиб имеет тенденцию к повторению вычислений. Это легко увидеть, если трассировать цель
?- фиб( 6, F).
На рис. 8.2 показано, как протекает этот вычислительный процесс. Например, третье число Фибоначчи f( 3) понадобилось в трех местах, и были повторены три раза одни и те же вычисления.
Этого легко избежать, если запоминать каждое вновь вычисленное число. Идея состоит в применении встроенной процедуры assert
для добавления этих (промежуточных) результатов в базу данных в виде фактов. Эти факты должны предшествовать другим предложениям, чтобы предотвратить применение общего правила в случаях, для которых результат уже известен. Усовершенствованная процедура фиб2
отличается от фиб только этим добавлением:
фиб2( 1, 1).
% 1-е число Фибоначчи
фиб2( 2, 1).
% 2-е число Фибоначчи
фиб2( N, F) :-
% N-e число Фиб., N > 2
N > 2,
Nl is N - 1, фиб2( N1, F1),
N2 is N - 2, фиб2( N2, F2),
F is F1 + F2,
% N-e число есть сумма
% двух предыдущих
asserta( фиб2( N, F) ). % Запоминание N-го числа
Эта программа, при попытке достичь какую-либо цель, будет смотреть сперва на накопленные об этом отношении факты и только после этого применять общее правило. В результате, после вычисления цели фиб2( N, F), все числа Фибоначчи вплоть до N-го будут сохранены. На рис. 8.3 показан процесс вычислении 6-го числа при помощи фиб2. Сравнение этого рисунка с рис. 8.2. показывает, на сколько уменьшилась вычислительная сложность. Для больших N такое уменьшение еще более ощутимо.
Запоминание промежуточных результатов - стандартный метод, позволяющий избегать повторных вычислений. Следует, однако, заметить, что в случае чисел Фибоначчи повторных вычислений можно избежать еще и применением другого алгоритма, а не только запоминанием промежуточных результатов.
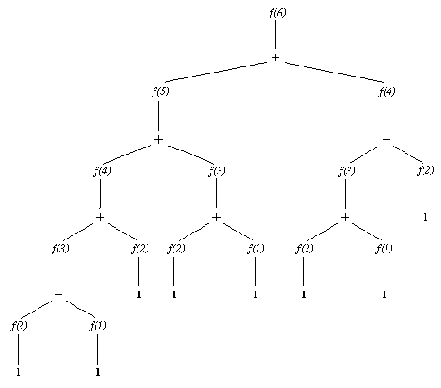
Рис. 8. 2. Вычисление 6-го числа Фибоначчи процедурой фиб.
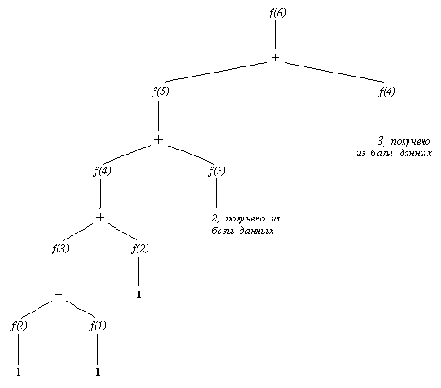
Рис. 8. 3. Вычисление 6-го числа Фибоначчи при помощи процедуры фиб2, которая запоминает предыдущие результаты. По сравнению с процедурой фиб здесь вычислений меньше (см. рис. 8.2).
Этот новый алгоритм позволяет создать программу более трудную для понимания, зато более эффективную. Идея состоит на этот раз не в том, чтобы определить N-e число Фибоначчи просто как сумму своих предшественников по последовательности, оставляя рекурсивным вызовам организовать вычисления "сверху вниз" вплоть до самых первых двух чисел.
Вместо этого можно работать "снизу вверх": начать с первых двух чисел и продвигаться вперед, вычисляя члены последовательности один за другим. Остановиться нужно в тот момент, когда будет достигнуто N-e число. Большая часть работы в такой программе выполняется процедурой
фибвперед( М, N, F1, F2, F)
Здесь F1 и F2 - (М - 1)-е и М-е числа, а F - N-e число Фибоначчи. Рис. 8.4 помогает понять отношение фибвперед. В соответствии с этим рисунком фибвперед находит последовательность преобразований для достижения конечной конфигурации (в которой М = N) из некоторой заданной начальной конфигурации. При запуске фибвперед все его аргументы, кроме F, должны быть конкретизированы, а М должно быть меньше или равно N. Вот эта программа:
фиб3( N, F) :-
фибвперед( 2, N, 1, 1, F).
% Первые два числа Фиб. равны 1
фибвперед( М, N, F1, F2, F2) :-
М >= N. % N-e число достигнуто
фибвперед( M, N, F1, F2, F) :-
M < N, % N-e число еще не достигнуто
СледМ is М + 1,
СледF2 is F1 + F2,
фибвперед( СледМ, N, F2, СледF2, F).
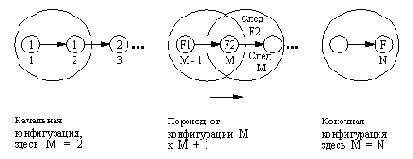
Рис. 8. 4. Отношения в последовательности Фибоначчи. "Конфигурация" изображается
здесь в виде большого круга и определяется тремя параметрами: индексом М и двумя
последовательными числами f( M-1) и f( М).
