Сцепление ( конкатенация)
Для сцепления списков мы определим отношение
конк( L1, L2, L3)
Здесь L1 и L2 - два списка, a L3 - список, получаемый при их сцеплении. Например,
конк( [а, b], [c, d], [a, b, c, d] )
истинно, а
конк( [а, b], [c, d], [a, b, a, c, d] )
ложно. Определение отношения конк, как и раньше, содержит два случая в зависимости от вида первого аргумента L1:
(1) Если первый аргумент пуст, тогда второй и третий аргументы представляют собой один и тот же список (назовем его L), что выражается в виде следующего прологовского факта:
конк( [ ], L, L ).
(2) Если первый аргумент отношения конк не пуст, то он имеет голову и хвост в выглядит так:
[X | L1]
На рис. 3.2 показано, как производится сцепление списка [X | L1] с произвольным списком L2. Результат сцепления - список [X | L3], где L3 получен после сцепления списков L1 и L2. На прологе это можно записать следующим образом:
конк( [X | L1, L2, [X | L3]):-
конк( L1, L2, L3).
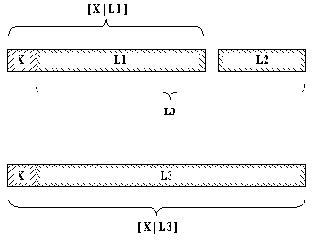
Рис. 3. 2. Конкатенация списков.
Составленную программу можно теперь использовать для сцепления заданных списков, например:
?- конк( [a, b, с], [1, 2, 3], L ).
L = [a, b, c, 1, 2, 3]
?- конк( [а, [b, с], d], [а, [ ], b], L ).
L = [a, [b, c], d, а, [ ], b]
Хотя программа для конк выглядит довольно просто, она обладает большой гибкостью и ее можно использовать многими другими способами. Например, ее можно применять как бы в обратном направлении для разбиения заданного списка на две части:
?- конк( L1, L2, [а, b, с] ).
L1 = [ ]
L2 = [а, b, c];
L1 = [а]
L2 = [b, с];
L1 = [а, b]
L2 = [c];
L1 = [а, b, с]
L2 = [ ];
no (нет)
Список [а, b, с] разбивается на два списка четырьмя способами, и все они были обнаружены нашей программой при помощи механизма автоматического перебора.
Нашу программу можно также применить для поиска в списке комбинации элементов, отвечающей некоторому условию, задаваемому в виде шаблона или образца. Например, можно найти все месяцы, предшествующие данному, и все месяцы, следующие за ним, сформулировав такую цель:
?- конк( До, [май | После ],
[янв, фев, март, апр, май, июнь,
июль, авг, сент, окт, ноябрь, дек]).
До = [янв, фев, март, апр]
После = [июнь, июль, авг, сент, окт, ноябрь, дек].
Далее мы сможем найти месяц, непосредственно предшествующий маю, и месяц, непосредственно следующий за ним, задав вопрос:
?- конк( _, [Месяц1, май, Месяц2 | _ ],
[янв, февр, март, апр, май, июнь,
июль, авг, сент, окт, ноябрь, дек]).
Месяц1 = апр
Месяц2 = июнь
Более того, мы сможем, например, удалить из некоторого списка L1 все, что следует за тремя последовательными вхождениями элемента z в L1 вместе с этими тремя z. Например, это можно сделать так:
?- L1 = [a, b, z, z, c, z, z, z, d, e],
конк( L2, [z, z, z | _ ], L1).
L1 = [a, b, z, z, c, z, z, z, d, e]
L2 = [a, b, z, z, c]
Мы уже запрограммировали отношение принадлежности. Однако, используя конк, можно было бы определить это отношение следующим эквивалентным способом:
принадлежит1( X, L) :-
конк( L1, [X | L2], L).
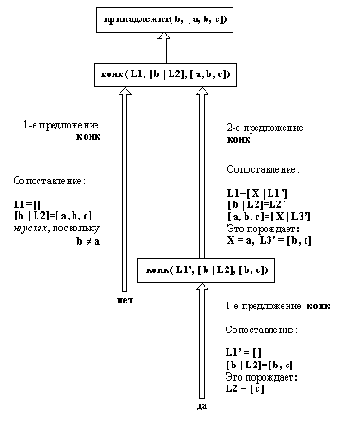
Рис. 3. 3. Процедура принадлежит1 находит элемент в заданном
списке, производя по нему последовательный поиск.
В этом предложении сказано: "X принадлежит L, если список L можно разбить на два списка таким образом, чтобы элемент Х являлся головой второго из них. Разумеется, принадлежит1 определяет то же самое отношение, что и принадлежит. Мы использовали другое имя только для того, чтобы различать таким образом две разные реализации этого отношения, Заметим, что, используя анонимную переменную, можно записать вышеприведенное предложение так:
принадлежит1( X, L) :-
конк( _, [X | _ ], L).
Интересно сравнить между собой эти две реализации отношения принадлежности. Принадлежит имеет довольно очевидный процедурный смысл:
Для проверки, является ли Х элементом списка L, нужно
(1) сначала проверить, не совпадает ли голова списка L с X, а затем
(2) проверить, не принадлежит ли Х хвосту списка L.
С другой стороны, принадлежит1, наоборот, имеет очевидный декларативный смысл, но его процедурный смысл не столь очевиден.
Интересным упражнением было бы следующее: выяснить, как в действительности принадлежит1 что-либо вычисляет. Некоторое представление об этом мы получим, рассмотрев запись всех шагов вычисления ответа на вопрос:
?- принадлежит1( b, [а, b, с] ).
На рис. 3.3 приведена эта запись. Из нее можно заключить, что принадлежит1 ведет себя точно так же, как и принадлежит. Он просматривает список элемент за элементом до тех пор, пока не найдет нужный или пока не кончится список.
